ROC-Kurven vergleichen mit JMP: Teil 1 – Grundlagen & Einzeltest mit Konfidenzband

Schlagwörter: ROC-Kurve, Sensitivität, Spezifität, AUC, Vorhersagemodelle, Cutoff-Wert, JMP Software, medizinische Statistik

Einführung: Was ist eine ROC-Kurve?

ROC-Kurven (Receiver Operating Characteristic) sind ein zentrales Werkzeug zur Bewertung von Klassifikationsmodellen, insbesondere in Bezug auf Sensitivität (True Positive Rate) und Spezifität (1 – False Positive Rate).

Vor einiger Zeit entwickelte mein Kollege Prof. Dr. Dr. David Meintrup ein hilfreiches Skript zur Analyse und zum Vergleich von ROC-Kurven in JMP. Mit diesem Add-In können Sie nicht nur eine einzelne ROC-Kurve mit Konfidenzbändern erzeugen, sondern auch mehrere Tests vergleichen.

Blog-Reihe in drei Teilen:

1. Teil 1: Grundlagen & ROC-Kurve mit Konfidenzband für einen Test

2. Teil 2: Den optimalen Cutoff-Wert identifizieren

3. Teil 3: Vergleich mehrerer Tests & partielle AUC (pAUC)

📚 Falls Sie neu in das Thema einsteigen: Eine gute Einführung finden Sie z. B. unter Introduction to ROC Analysis.

Beispiel-Datensatz: aSAH aus dem R-Paket „pROC“

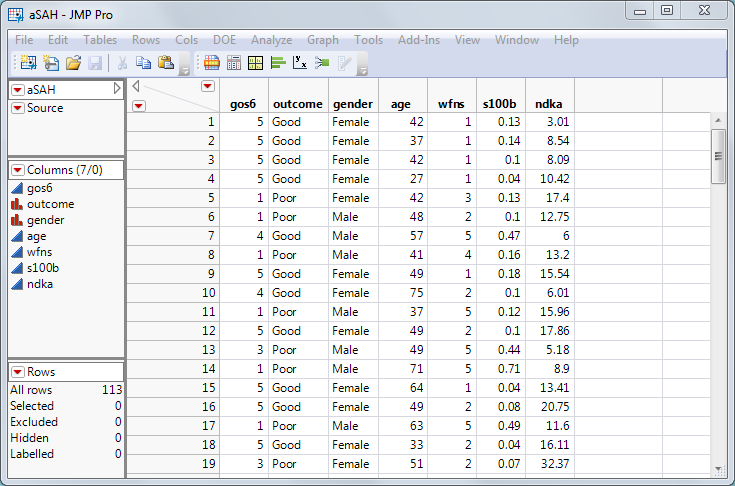
Zur Veranschaulichung nutzen wir den aSAH-Datensatz (aneurysmatische Subarachnoidalblutung) mit 113 Patienten. Ziel: Ein klinischer Test, der zuverlässig den Outcome (Prognose) eines Patienten vorhersagt. Ein schlechter Ausgang erfordert meist intensivere medizinische Versorgung [1].

Drei Tests stehen zur Auswahl:

• wfns

• s100b

• ndka

Fragestellung: Welcher Test ist am besten geeignet, um Patienten mit schlechter Prognose zu erkennen?

Ein „guter Test“ erfüllt zwei Kriterien:

• Hohe Sensitivität: erkennt zuverlässig Patienten mit schlechtem Ausgang

• Niedrige Falsch-Positiv-Rate: klassifiziert möglichst keine gesunden Patienten falsch

Eine ROC-Kurve zeigt das Zusammenspiel von Sensitivität und Falsch-Positiv-Rate in einem einzigen Diagramm – ideal zur Bewertung und zum Vergleich diagnostischer Tests.

Anwendung: ROC-Kurve für „wfns“ in JMP erstellen

Starten Sie das JMP-Skript. Ein Dialogfenster erscheint:

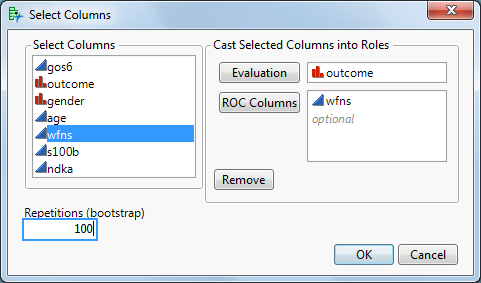
• Evaluation-Spalte: enthält das Ziel (Outcome), z. B. „Gut“ vs. „Schlecht“

• ROC-Spalten: mindestens ein Test, z. B. wfns
  (Hinweis: Bei Vorhersagemodellen wie Logistische Regression, Random Forest etc. hier die vorhergesagten Wahrscheinlichkeiten verwenden.)

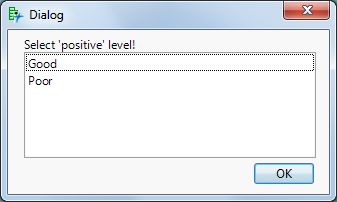
Nach Klick auf OK folgt ein zweites Dialogfeld: Dort geben Sie an, welcher Wert als „positiv“ gelten soll – in unserem Fall „Poor“ (schlechter Outcome).

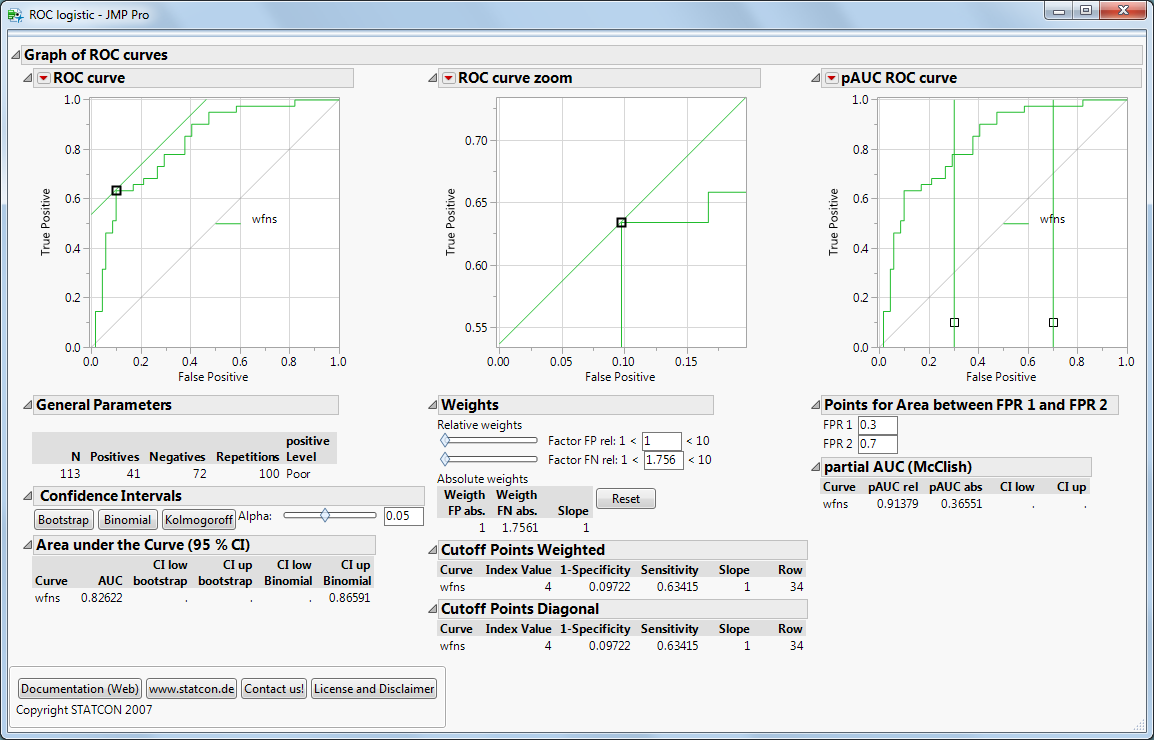
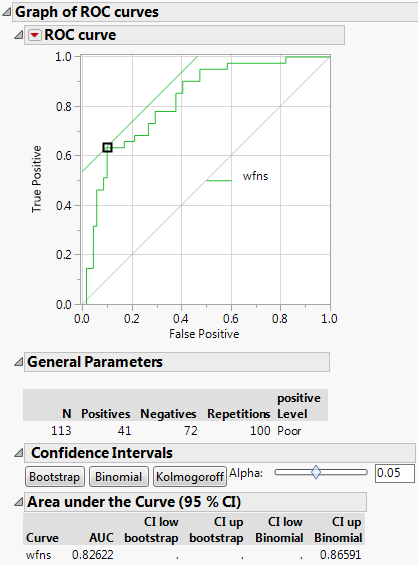
Interpretation: AUC & Konfidenzbänder

• Die AUC (Area Under the Curve) beträgt 82 % – ein guter Wert, abhängig vom Anwendungsfall.

• Eine perfekte Vorhersage hätte AUC = 1.0.

• Die AUC eignet sich besonders gut zum Vergleich mehrerer Tests.

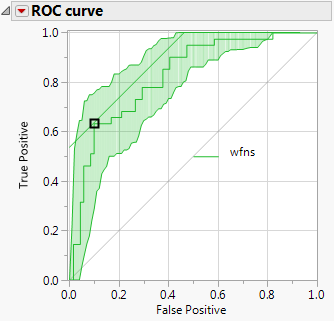
Jetzt auf „Bootstrap“ klicken!

JMP erstellt grüne Konfidenzbänder um die ROC-Kurve. Diese zeigen, wie stabil und verlässlich der Test ist.

• Ist die ROC-Kurve deutlich über der Diagonale (Zufallsmodell), ist der Test gut.

• In unserem Fall liegt die Diagonale außerhalb der Konfidenzbänder – ein starkes Signal.

Warum sind die Bänder nicht symmetrisch? Wir verwenden hier Bootstrap-Konfidenzbänder. Alternativ gibt es binomiale oder Kolmogorov-Bänder (klassisch symmetrisch).

Ausblick: Cutoff-Wert & Testvergleich

Im nächsten Blogbeitrag gehen wir auf die Auswahl des optimalen Cutoffs ein. Danach zeigen wir, wie Sie mehrere Tests mithilfe von ROC-Kurven und partiellen AUCs (pAUC) vergleichen können.

Literatur & Ressourcen

• X. Robin et al.: pROC: An open-source package for R and S+ to analyze and compare ROC curves

• M. Müller et al.: ROC-Analyse in der medizinischen Diagnostik

• JMP 12 Dokumentation